Função do 1 grau e seu gráfico (Função Afim)

 

 

,

onde

a é o coeficiente angular, que determina a inclinação da reta;

b é o coeficiente linear, que determina o ponto onde a reta intercepta o eixo y.  

 

• Função do 1º grau crescente (a>0)

 

Neste caso o gráfico possui o seguinte comportamento:

 

 

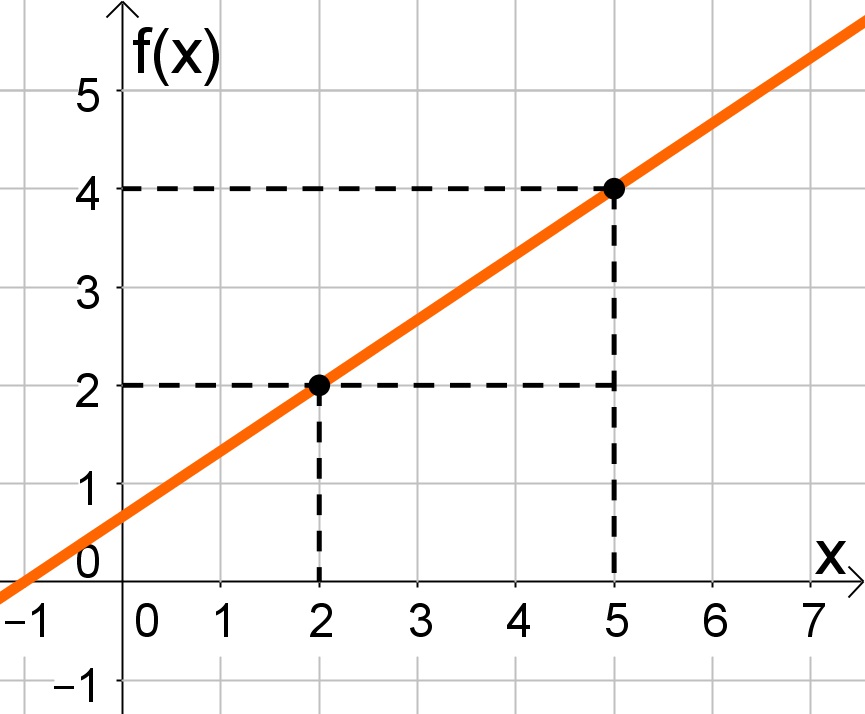
Para verificar, pode-se construir a função que está plotada no gráfico a cima da seguinte forma. 

 

a) Encontrar o coeficiente angular com a fórmula dada anteriormente:

 

.

 

b) Encontrar o coeficiente linear, para isto utiliza-se a forma básica, , o ponto  e o coeficiente angular recém encontrado :  

.

 

Assim, encontramos a função  que representa a função do gráfico, onde a>0.

• Função do 1º grau decrescente (a<0)

 

Neste caso o gráfico possui o seguinte comportamento:

 

 

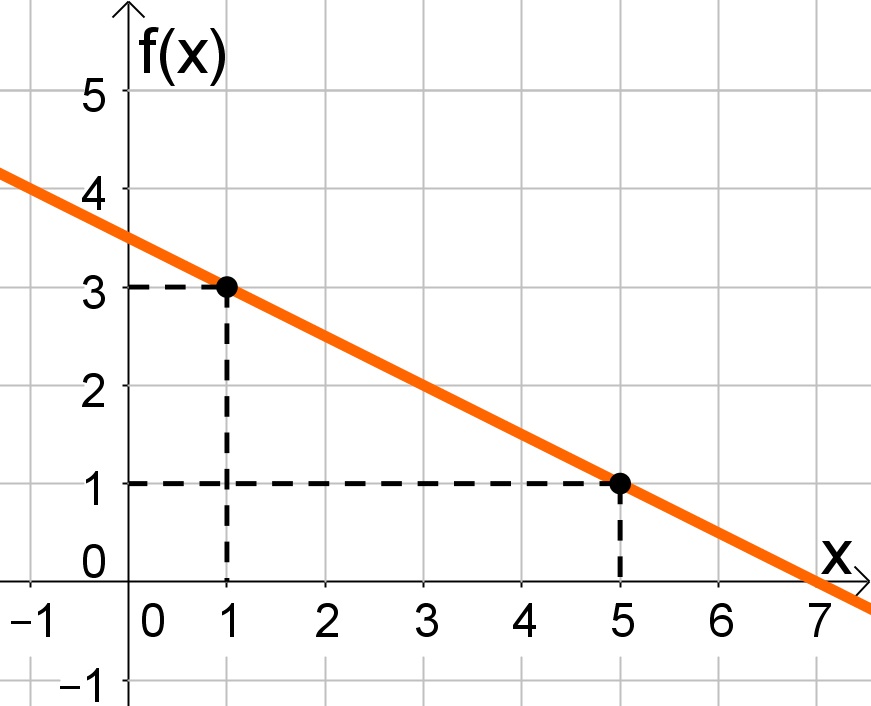
Para verificar, repeti-se o procedimento realizado no caso a cima.

 

a) Encontrar o coeficiente angular:

 

.

 

b) Encontrar o coeficiente linear, para isto utilizaremos a forma básica, o ponto  e o coeficiente angular : 

 

.

 

Assim, encontra-se a função  que representa a função do gráfico, onde a<0.