Função do 2º grau ou função quadrática

 

Conhecemos como função quadrática ou função do 2º grau a função com domínio e contradomínio nos reais e que a lei de formação é f(x) = ax² +bx + c.

 

 

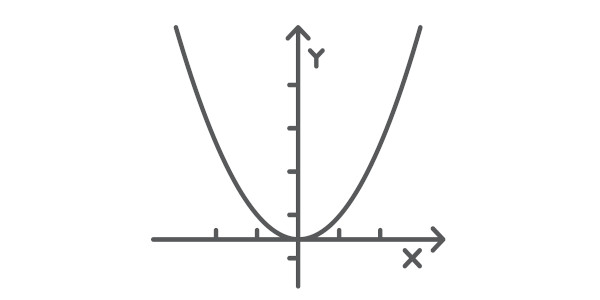
Definimos como função do 2º grau, ou função quadrática, a função R → R, ou seja, uma função em que o domínio e o contradomínio são iguais ao conjunto dos números reais, e que possui a lei de formação f(x) = ax² +bx +c.

 

O gráfico da função quadrática é sempre uma parábola e possui elementos importantes, que são:

 

• as raízes da função quadrática, calculadas pelo x’ e x”;

• o vértice da parábola, que pode ser encontrado a partir de fórmulas específicas.

O que é uma função do 2º grau?

 

Uma função polinomial é conhecida como função do 2º grau, ou também como função quadrática, quando em sua lei de formação ela possui um polinômio de grau dois, ou seja, f(x) = ax² +bx +c, em que a, b e c são números reais, e a ≠ 0. Além da lei de formação, essa função possui domínio e contradomínio no conjunto dos números reais, ou seja, f: R→ R.

 

Exemplos

 

a) f(x) = 2x²+3x + 1

 

a = 2

b = 3

c=1

 

b) g(x) = -x² + 4

 

a = -1

b = 0

c = 4

 

c) h(x) = x² – x

 

a = 1

b = -1

c = 0

Valor numérico de uma função

 

Para encontrar o valor numérico de qualquer função, conhecendo a sua lei de formação, basta realizarmos a substituição do valor de x para encontrar a imagem f(x).

 

Exemplos

 

Dada a função f(x) = x² + 2x – 3, calcule:

 

a) f(0)
f(0) = 0² +2·0 – 3 = 0 + 0 – 3 = –3

b) f(1)
f(1) = 1² + 2·1 + 3  = 1+2 – 3 = 0

c) f(2)
f(2) = 2² + 2·2+3 = 4+4–3=5

d) f(-2)
f(-2) = (-2)² + 2·(-2) – 3
f(-2) = 4  - 4 – 3 = –3

Raízes da função de 2º grau

 

Para encontrar as raízes da função quadrática, conhecidas também como zero da função, é necessário o domínio das equações do segundo grau. Para resolver uma equação do segundo grau, há vários métodos, como a fórmula de Bhaskara e a soma e produto.

A raízes de uma função quadrática são os valores de x que fazem com que f(x) = 0. Sendo assim, para encontrar as raízes de uma equação do 2º grau, faremos ax² + bx + c = 0.

 

Exemplo

 

f(x) = x² +2x – 3

a = 1

b = 2

c = –3

Δ =b² – 4ac

Δ=2² – 4 ·1·(-3)

Δ=4 +12

Δ = 16

 

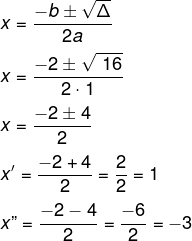
Então, os zeros da função são {1, -3}.

 

O valor do delta nos permite saber quantos zeros a função quadrática vai ter. Podemos separar em três casos:

 

• Δ > 0 → a função possui duas raízes reais distintas;

• Δ = 0 → a função possui uma única raiz real;

• Δ < 0 → a função não possui raiz real.

 

Gráfico de uma função do 2º grau

 

O gráfico de uma função do 2º grau é representado sempre por uma parábola. Existem duas possibilidades, dependendo do valor do coeficiente “a”: a concavidade da parábola pode ser para cima ou para baixo.

 

Se a > 0, a concavidade é para cima:

 

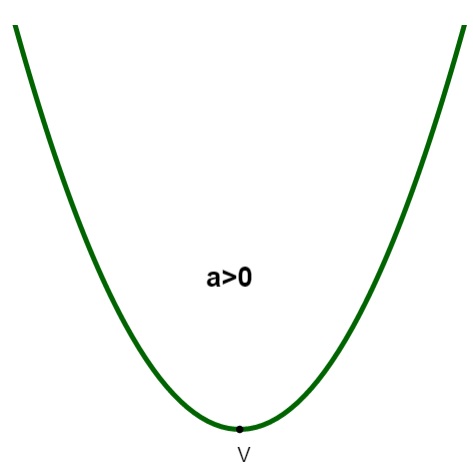
O ponto V representa o que conhecemos como vértice da parábola, que, nesse caso, é o ponto de mínimo, ou seja, o menor valor que f(x) pode assumir.

 

Se a < 0, a concavidade é para baixo:

 

 

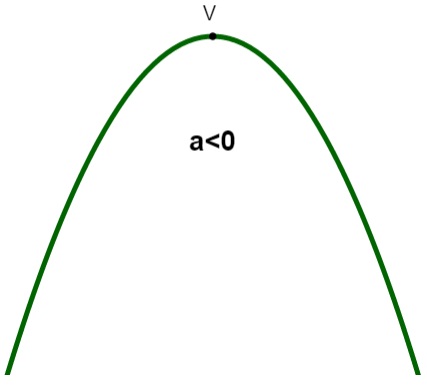
Quando isso ocorre, perceba que, nesse caso, o vértice é o ponto de máximo da função, ou seja, maior valor que f(x) pode assumir.

 

Para fazer o esboço do gráfico, precisamos encontrar:

 

• os zeros da função;

• o ponto em que a função intercepta o eixo y;

• o ponto de máximo ou de mínimo da parábola, que conhecemos como vértice da parábola.

Vértice da parábola

 

Como vimos anteriormente, o vértice da parábola é o ponto de mínimo ou de máximo do gráfico. Para encontrar o valor de x e y no vértice, utilizamos uma fórmula específica. Vale ressaltar que o vértice é um ponto V, logo ele possui coordenadas, representadas por x_v e y_v.

 

Para calcular o valor de V (x_v, y_v), utilizamos as fórmulas:

 

 

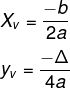
Exemplo

 

Encontre o vértice da parábola f(x) = –x² +4x – 3.

 

a = -1.

b = 4.

c = -3

 

Calculando o Δ e aplicando a fórmula de Bhaskara, temos que:

 

Δ=b² – 4ac

Δ=4² – 4(-1) (-3)

Δ=16 – 12

 Δ=4

 

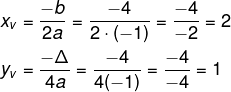
Representação gráfica de uma função do 2º grau

 

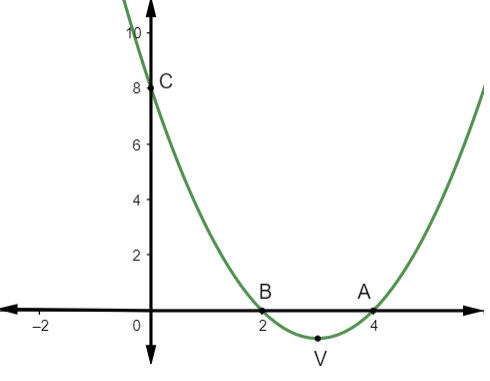
Para realizar o esboço do gráfico de uma função, é necessário encontrar três elementos: os zeros ou raízes da função, o vértice e o ponto em que a função toca o eixo y, conforme o exemplo a seguir.

 

Exemplo

 

f(x) = x² – 6x + 8

 

1º passo: As raízes da função são os pontos em que a parábola toca o eixo x, logo queremos encontrar os pontos (x’, 0) e (x”,0).

 

Para isso faremos f(x) = 0, então temos que:

 

x² – 6x + 8=0

a= 1

b= -6

c = 8

Δ = b² -4ac

Δ = (-6)² -4·1·8

Δ = 36 – 32

Δ = 4

 

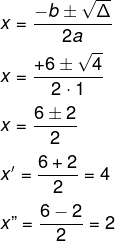
Já temos dois pontos para o gráfico, o ponto A(4,0) e o ponto B (2,0).

 

2º passo: encontrar o vértice da parábola.

 

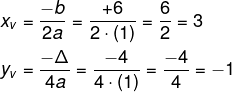
Então o vértice da parábola é o ponto V(3, -1).

 

3º passo: encontrar o ponto de intersecção da parábola com o eixo y.

Para isso, basta calcular f(0):

 

f(x) =x² – 6x + 8

f(0) = 0² -6·0 + 8

f(0) = 8

Por fim, o ponto C (0,8) pertence ao gráfico.

 

4º passo: Agora que temos os pontos, vamos marcá-los no plano cartesiano e fazer o esboço do gráfico da parábola.

 

A(4,0)

B(2,0)

V(3,-1)

C(0,8)